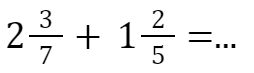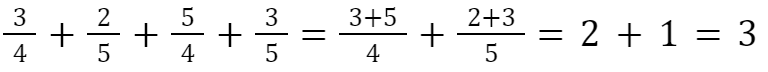Lecția 9: Adunarea și scăderea fracțiilor
(Durata: 2 ore)
Scop
Elevii vor putea rezolva probleme, situații care solicită însumarea părților sau suma unor fracții ordinare, precum și diferențe de fracții ordinare.
Competențe specifice
2.2. Efectuarea de calcule cu fracţii folosind proprietăţi ale operaţiilor aritmetice
3.2. Utilizarea de algoritmi pentru efectuarea operaţiilor cu fracţii ordinare sau zecimale
5.2. Analizarea unor situaţii date în care intervin fracţii pentru a estima sau pentru a verifica validitatea unor calcule
6.2. Reprezentarea matematică, folosind fracțiile, a unei situaţii date, în context intra și interdisciplinar (geografie, fizică, economie etc.)
Neînțelegeri / greșeli tipice
Unii elevi adună numitorii între ei sau nu urmează algoritmul de însumare, având erori la determinarea numitorului comun.
Întrebări esențiale
Cum putem însuma sau scădea părți ale unui întreg?
Cum adunăm sau scădem două sau mai multe numere scrise sub forma fracțiilor ordinare?
Note
În această lecție, pornind de la reprezentarea grafică a fracțiilor ordinare, elevii deprind regulile pentru a aduna sau scădea două fracții ordinare.
Prin problemele propuse, elevii vor rezolva situații problemă din contexte reale utilizând adunarea și scăderea fracțiilor ordinare.
Intro
Continuați discuția din lecția trecută despre problema călușarilor - ce întrebări au ridicat dificultăți? Rugați elevii să reia strategiile de comparare a fracțiilor învățate.
Propuneți elevilor următoarea problemă:
În format brainstorming căutăm modalitățile de rezolvare a problemei și determinăm problemele pe care le putem întâmpina în rezolvare. Colectați întâi răspunsurile elevilor, apoi treceți prin ele și eliminați neînțelegerile comune.
Prima problemă apărută este de a determina cât au mâncat Mihai și Ana împreună. Apoi trebuie să aflăm ce parte din pizza a rămas pentru cățel.
Răspunsul la această problemă solicită introducerea operațiilor de adunare și scădere cu fracții ordinare.
Partea rămasă dintr-un întreg este de o optime, deci cățelul va primi o optime de pizza.
Cuprins
Împărțiți clasa în grupe de câte 3-4 elevi. Fiecare grupă primește două fracții. Unele grupe primesc două fracții cu același numitor, celelalte primesc două fracții cu numitori diferiți.
Cereți grupelor să reprezinte cele două fracții, apoi să încerce să stabilească cât este suma lor folosind imaginile create.
La prezentarea rezultatelor solicitați întâi grupele care au avut numitor comun.
Ulterior prezentării deduceți împreună cu elevii regula de adunare.
Apoi, prezintă grupele care au primit perechi de fracții cu numitori diferiți.
În mod analog deduceți regula de însumare.
Fișă de lucru: Adunarea fractiilor ordinare 1 (Liveworksheets)
După completarea fișei, veți propune elevilor să rezolve următorul exercițiu:
Analizând exercițiul, elevii constată o diferență: fracții mixte ca termeni ai adunării. Pentru a putea efectua operația cu algoritmul precedent, ei vor introduce întregii în fracție, astfel:
De remarcat că vom obține același rezultat separând părțile întregi:
Vorbind despre adunarea unor numere să amintim elevilor proprietățile adunării, pe care le exemplificăm:
asociativitate: pentru orice numere a, b și c, avem: (a+b)+c=a+(b+c);
comutativitate: pentru orice numere a și b, avem: a + b = b + a;
0 este element neutru: pentru orice număr a, avem: a + 0 = 0 + a = a (0 poate fi scris ca fracție ordinară ca 0/n, unde n este un număr natural nenul).
Aplicare
Subliniați marea idee că putem folosind comutativitatea și asociativitatea, simplificând astfel calculele. Flosiți exerciții precum:
În mod similar, amintiți elevilor că proba adunării este scăderea: un termen se determină ca diferența dintre sumă și celălalt termen. Rezultă că putem introduce scăderea fracțiilor ordinare.
Deduceți folosirea aceluiași algoritm ca în cazul adunării.
Elevii exersează folosind fișa Scăderea fracților ordinare.
Diferențiere
Încheiere
Dacă timpul permite, începeți să discutați frontal fișa Probleme cu adunări și scăderi de fracții ordinare - sunt 6 probleme care urmăresc două competențe - „traducerea” în limbaj matematic a unei situații din viața reală și efectuarea corectă a adunării și scăderii cu fracții ordinare diverse.
Oferiți ca bonus testul de autoevaluare pentru acasă, pentru ca elevii să își verifice neînțelegerile.
Resurse descărcabile
Adunarea fractiilor ordinare 1 (Liveworksheets)
Scăderea fracților ordinare (pdf)
Probleme cu adunări și scăderi de fracții ordinare (pdf)
Test autoevaluare (docx)
Autori
Marius Lobază
Categorii
Clasa a V-a, Fracții ordinare
Material realizat sub licență Creative Commons 4.0 CC BY-NC-SA Atribuire-Necomercial-Partajare în Condiții Identice (puteți folosi materialul gratuit cu menționarea sursei)